Codificació de Informació.

0. Introducció
Una informació es codifica en grups de dades per tal de poder ser guardada, transmessa i modificada.
La codificació cap a un ordinador es realitza amb codi binari, sempre seguint uns patrons establerts per tal de que aquesta no perdi el seu significat. Un 24 ha de ser un 24 en binari o en decimal.
Els grups de dades de informació codificada es poden mesuran en bits, bytes, kilobtyes, megabytes, ….
Aquests grups de dades podran ser descodificats i codificats per programes preparats per manipular el tipus de informació en qüestió.
Existeixen codificacions que encapsulen una dada per tal de poder ser comprovada i corregida.
Per la transmissió es segueix la teoria del model TCP/IP o el model de capes OSI on es basen quasi tots els sitemes de comunicació que s’empren avui en dia.
Aquests models exposen la transformació de dades desde la capa física fins a la capa d’aplicació.
Si ens fixam en la teoria de la comunicació, així de simple:
emisor (missatge)->(canal)-(missatge)->recepetor(missatge).
Sempre és la teoria que hem vist moltes vegades, és aquesta teoria, enviar un missatge d’un lloc a un altre.
En aquesta teoria hi hem d’afegir que els responsables de transmetre aquests missatges són màquines i, per tant, han de tenir ben establerts els protocols de comunicació. Noltros veurem unes pinzellades d’alguns detalls importants.
1. Codificació del missatge.
Sabem que un computador, al ser un element electrònic, té més facilitat en emprar codi binari. Encés, apagat és més fàcil d’entendre que 5,4 ó 5,5 ó 5,6 quan es tracta d’electricitat no es pot assegurar que el nombre sigui 5 ó 6.
- S’ha de conèixer la natura dels nombres binaris, la següent taula mostra un nombre binari de quatre bits i el seu nombre decimal equivalent.
| p3 | p2 | p1 | p0 | Nombre decimal |
| 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 0 | 1 | 1 |
| 0 | 0 | 1 | 0 | 2 |
| 0 | 0 | 1 | 1 | 3 |
| 0 | 1 | 0 | 0 | 4 |
| 0 | 1 | 0 | 1 | 5 |
| 0 | 1 | 1 | 0 | 6 |
| 0 | 1 | 1 | 1 | 7 |
| 1 | 0 | 0 | 0 | 8 |
| 1 | 0 | 0 | 1 | 9 |
| 1 | 0 | 1 | 0 | 10 |
| 1 | 0 | 1 | 1 | 11 |
| 1 | 1 | 0 | 0 | 12 |
| 1 | 1 | 0 | 1 | 13 |
| 1 | 1 | 1 | 0 | 14 |
| 1 | 1 | 1 | 1 | 15 |
- Amb un grup de N nombres binaris es poden codificar 2eN elements, per exemple amb un grup de quatre binaris podem codificar 2e4 = 2*2*2*2 = 16 elements, normalment del 0 al 17. Amb dos nombres binaris podrem codificar 4 elements.
- Els nombres binaris s’agrupen i tenen mides concretes, així es pot descodificar el seu codi. Per mesurar tenim: bit (1binari), Byte(8bits),KB(512Bytes),MB(1024Bytes),GB(1024MB),…
- Amb els nombres binaris no sols codificam decimals, es codifiquen molts altres codis. Observa la següent taula.
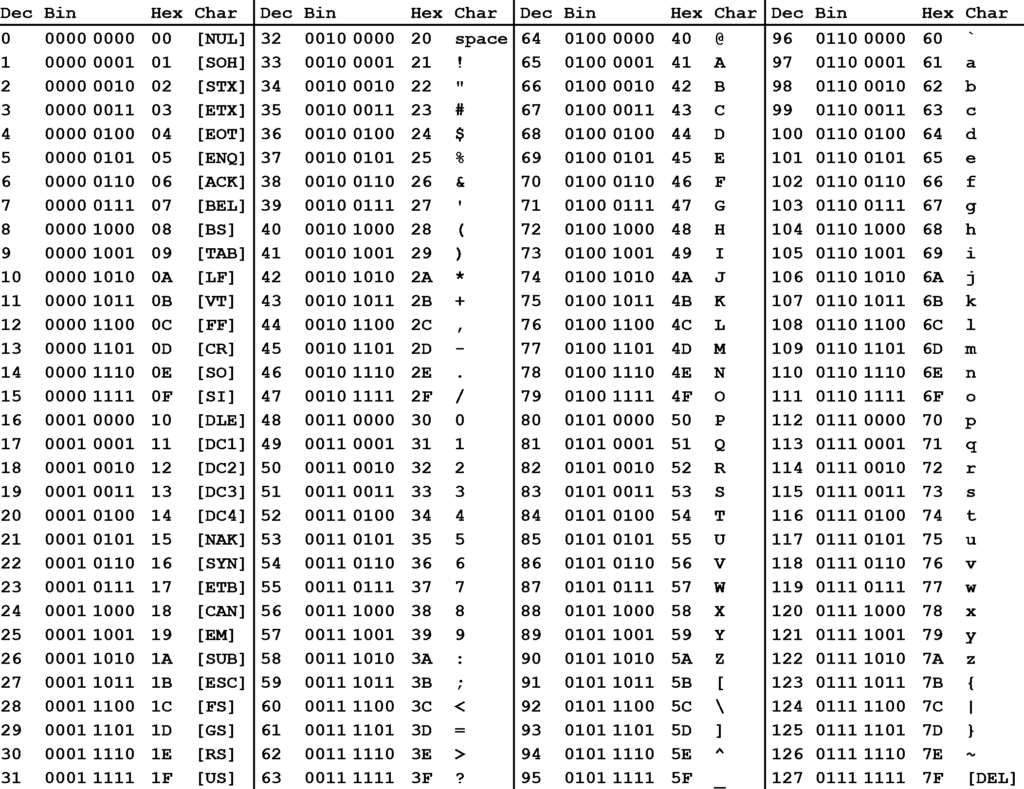
Exercicis de codificació de missatges:
- Cerca i escriu els missatge “BON DIA” en binari.
- Quines codificacions has usat a l’exercici anterior?
- Passa de Dec a Char: “110 111 115 111 109 98 105 110 97 114 105”. Afegeix els espais que li falten.
- Dins un ordinador què pesa més,el Hex ’61’ o el Char ‘a’?
- Què és i que significa ASCII? Cerca una imatge del codi ASCII.
- Quants elements es poden codificar amb 32 bits?
- Quants de Bytes hi ha dins un MByte? i quants de bits?
- 4MB són ___ KBytes.
Altres codificacions.
Els tipus de codificacions s’han d’adaptar a les informacions que es volen representar. Si volem representar nombres negatius (component a1, componenta2, ..) , nombres Reals (coma flotant), … Així cada tipus de codificació representa una tipus informació i té un pes concret.
Tipus java: https://www.w3schools.com/java/java_data_types.asp
Tipus Javascript: https://www.w3schools.com/js/js_datatypes.asp
2. Detecció i Correcció d’errors en un missatge.
Una codificació pot tenir errors. O sigui ‘A’ quan el guardem no sigui ‘A’ i sigui un altre codi.
Els missatges poden tenir errors degut a una atenuació, distorsió, interferència o renou. Sigui quina sigui la causa, necessitarem comprovar que les dades codificades siguin correctes i que no canviin el contingut de la informació.
Sigui pel cas que sigui no ha de passar que codifiquem “01000001” i arribi “01010001”.
Veurem dues codificacions, un ens detecta l’error, l’altre el detecta i el pot corregir. Ambdues afegeixen bits redundants.

a)Detecció d’errors. Bit de paritat.
Afegint un bit a la codificació podem detectar si hi ha un error.
Codificació:
Si ho aplicam sobre el codi ASCII de la nostra taula, sols usa 7bits. Emprarem el bit de l’esquerra per afegir el bit de paritat, i
- Si el nombre de 1’s del codi original es parell el bit de paritat serà 0.
- Si el nombre de 1’s del codi original es senar el bit de paritat serà 1.
Exemples:
r: “1110010”, 4 1’s -> “01110010”
s: “1110010”, 5 1’s -> “11110010”
Detecció d’errors:
Per detectar si hi ha un error contarem el nombre be 1’s si és imparell voldrà dir que hi ha un error en algún bit.
Exemples:
“1110010”-> sense cap error -> tenim r.
“0110010”->existeix un error. No està ben codificat.
Exercicis:
- Codifica les lletres MISSATGE amb bits de paritat. Quants de bits ocupa? Quants de bits ha augmentat el seu pes?

b) Correcció d’errors. Codi Hamming.
Per detectar i corregir un error es necessari afegir més bits al codi, afegim una espècie de cuirassa preparada, ens generarà més redundància. El missatge codificat podrà ser recuperat davant impertinències.
*Qualsevol…., no es tan així, pot ser que l’atac sigui ferotge i el nostre missatge quedi xafadíssim.
El codi Hamming té diferents nivells de codificació, aquests es poden augmentar o disminuir depenent del coneixement de les impertinències que pugui sofrir.
Codificació
Treballarem a nivell Hamming(7,4) on s’envien 7 bits on 4 són de dades, el “helmet” que li proporcionam és de 3.
Es defineix un patró de bits de paritat que permet reconèixer un error i també pot trobar on és.
El codi que enviam queda enmig dels bist de paritat que es col·loquen seguint l’exponencial de 2, quedant a les posicions 1,2,4.
Si tenim el codi a codificar: c0.c1.c2.c3
| P0 | P1 | C0 | P2 | C1 | C2 | C3 | Càlcul de codificació | |
| X | X | X | X | càlcul de paritat per P0: (C0+C1+C3) si parell 0, sino 1 | ||||
| X | X | X | X | càlcul de paritat per P1: (C0+C2+C3) si parell 0, sino 1 | ||||
| X | X | X | X | càlcul de paritat per P2: (C1+C2+C3) si parell 0, sino 1 |
Exemple:
Volem codificar el codi 1011 en Hamming (7,4).
| P0 | P1 | C0 | P2 | C1 | C2 | C3 | Càlcul de codificació | |
| X | 1 | 0 | 1 | càlcul de paritat per P0: (C0+C1+C3)=2 => P0= 0 | ||||
| X | 1 | 1 | 1 | càlcul de paritat per P1: (C0+C2+C3)=3 => P1=1 | ||||
| X | 0 | 1 | 1 | càlcul de paritat per P2: (C1+C2+C3)=2 => P2=0 | ||||
| 0 | 1 | 1 | 0 | 0 | 1 | 1 | MISSATGE CODIFICAT |
RESULTAT= 0110011
Verificació i Correcció.
Quans arriba un missatge s’ha de saber amb quin tipus de codificació està generat. Una vegada es sap, el que s’ha de fer és descodificar. En el nostre cas recuperarem la informació de dins d’una dada Hamming(7,4), d’on treurem la dada i, si és necessari, la corregirem.
Per corregir, ens fixarem les files afectades per la incorrecció. D’elles s’ha de mirar quines columnes estan afectades, o sigui quin bit és que està girat. Una vegada es troba es gira i ja es té la solució.
Exemple:
- Ens envien la dada 1101001.
P0 P1 C0 P2 C1 C2 C3 Càlcul de codificació 1 1 0 1 0 0 1 correcció x x x x p1. correcte x x x x p2.correcte x x x x p3.correcte x x x x resultat: 0001
| 0 | 0 | 0 | 1 | 1 | 1 | 0 | correcció |
| x | x | x | x | p1. incorrecte | |||
| x | x | x | x | p2.incorrecte | |||
| x | x | x | x | p3.incorrecte | |||
| resultat: ??¿? |
En aquest cas, la dada llegida no és correcte…, que vol dir? es pot corregir? sí!
- S’ha de mirar quines files estan afectades per la incorrecció.
- Es troben les columnes comuns, en aquest cas és la columna de la dreta.
- Giram el bit coincident i ens queda el codi codificat correcte: 0001111.
3. Un altre exemple. 1111001
| P0 | P1 | C0 | P2 | C1 | C2 | C3 | Càlcul de codificació |
| 1 | 1 | 1 | 1 | 0 | 0 | 1 | correcció |
| x | x | x | x | p1. incorrecte | |||
| x | x | x | x | p2.incorrecte | |||
| x | x | x | x | p3.correcte | |||
| resultat¿??¿ |
- fila afectada la C0.
- per tant el codi quedarà 1101001 , i el contingut és: 0001.
- Codifica la paraula “MareMar” en Hamming(7,4)
- Corregeix: 0110011, 1100110, 0011001.
NO EDITAT—–
Nosaltres treballarem sobre la que s’anomena la capa d’aplicació, les capes de devall són per oferir un transport confiable, és a dir, cada capa ofereix confia en les altres ja que “existeix un protocol establert entre cada una de les capes”.

https://webftp.dondominio.com/
Servidor FTP: ftp.gimnesia.net
Cada alumne tendra un espai accessible mitjançant un ftp a aula.gimnesia.net, aquí hi ha les credencials que s’han generat https://docs.google.com/document/d/e/2PACX-1vTs7ML71HcQZUkCS4lWMo7ZU3t8Tmg4pftefFR98avQpSIbpbRmaDlPDaKMsVsUKkMW7X_6-QseMQvf/pub