U8. l’interior dels ALGORITMES.
Llenguatges de programació
Un programa és un algorisme expressat de tal manera que un computador el pot entendre i executar. Hem insistit molt en el fet de que els computadors operen en llenguatge binari, i per a ells solament existeixen seqüències de 0 i 1. Per exemple, una operació bàsica com una suma es expressada per la màquina amb tres seqüències de ceros i uns: una seqüència per a cadascun dels operands i altra per a l’operador suma. Aquestos són els anomenats codis de màquina.
ba 0c 01
b4 09
cd 21
b8 00 4c
cd 21
48 65 6c 6c 6f 2c
20 57 6f 72 6c 64
21 0d 0a 24
Aquesta manera de comunicar-se amb la màquina resulta molt complicada per als humans, ja que cal recordar el codi corresponent a cadascuna de les operacions que la CPU pot realitzar. Per aquest motiu es va desenvolupar un llenguatge que permetera substituir alguns codis màquina per símbols fàcils de recordar com ADD per a la suma: el llenguatge assemblador.
.model small
.stack
.data
saludo db "Hola mundo!!!", "$"
.code
main proc ;Inicia proceso
mov ax,seg saludo ;hmm ¿seg?
mov ds,ax ;ds = ax = saludo
mov ah,09 ;Function(print string)
lea dx,saludo ;DX = String terminated by "$"
int 21h ;Interruptions DOS Functions
;mensaje en pantalla
mov ax,4c00h ;Function (Quit with exit code (EXIT))
int 21h ;Interruption DOS Functions
main endp ;Termina proceso
end main
De tota manera, encara que el llenguatge assemblador simplifica la programació una mica, aquesta continua sent una tasca complicada, ja que cal dir-li a la CPU totes i cadascuna de les operacions que cal fer una per una. També hi ha un altre problema: el llenguatge assemblador és diferent per a cada arquitectura concreta de computador, per la qual cosa cal re-escriure els programes per a que funcionen en diferents models de processadors.
Per resoldre els problemes del llenguatge assemblador i facilitar la creació de programes aparegueren, a finals de la dècada de 1950, els llenguatges de programació d’alt nivell. Aquestos llenguatges permetien escriure programes més simples i comprensibles, vàlids per diferents computadors i, en ocasions, per a diferents sistemes operatius.
El llenguatge de codis de màquina es considera un llenguatge de “baix nivell” per què és el que utilitza la màquina, mentre que el llenguatge assemblador és considerat un llenguatge de nivell intermedi, ja que s’acosta més al llenguatge dels humans. Els llenguatges de programació moderns més utilitzats es consideren de “alt nivell” ja que són similars al llenguatge natural dels humans.
El primer llenguatge d’alt nivell va ser FORTRAN, un llenguatge especialment adaptat per al càlcul numèric i la computació científica, però prompte aparegueren multitud de llenguatges com ADA, ALGOL, BASIC, C, COBOL, Java, Lisp, Pascal, Perl, PHP, Python, etcètera.
Cadascun d’aquestos llenguatges era de propòsit general o bé estava especialment adaptat a la resolució d’un tipus particular de problema (per exemple LISP a la intel·ligència artificial). Molts d’aquestos llenguatges han sigut abandonats, mentre que la importància d’altres ha augmentat. També han canviat els paradigmes de programació, passant de la programació estructurada a la més moderna programació orientada a objectes.
Programació estructurada
La programació estructurada pretén que els programes no solament funcionen, sinó que estiguen escrits de manera que facilite la seua lectura posterior. Segons aquest mètode de programació, qualsevol programa pot ser escrit utilitzant únicament tres tipus d’estructures (que hem vist anteriorment):
- Seqüències
- Condicionals
- Iteracions o repeticions
Els programes es dissenyen de manera modular, separant les parts complexes del programa en segments que poden ser més tard re-utilitzats, i descendent, resolent els problemes de manera ordenada des del més general fins als més particulars.
ALGORITME.
Un algoritme és una sequencia de instruccions que s’encarreguen de sol·lucionar un problema. Per fer l’esbós d’un algoritme existeixen eines, aquestes ajuden a comunicar i entendre el seu funcionament, eines com el diagrama de fluxe i el pseudocodi, serveixen per concretar i comunicar solucions, no implementen cap programa, sols indiquen els camins i que seguirà un algoritme.
Sempre es convenient fer una explicació textual i comentada tant del problemea com de la solució que proporciona l’algoritme.
Pseudocodi i ordinogrames
El pseudocodi i els ordinogrames seran les dues eines que s’empren per expressar algorismes. Són les maneres que pots utilitzar per dissenyar “en brut” un algorisme sense tenir que pensar en la sintaxi d’un llenguatge de programació concret.
Pseudocodi
El pseudocodi no és un llenguatge de programació però tampoc té la llibertat del llenguatge col·loquial. En realitat és una forma d’expressar els algorismes on es segueixen una serie de normes i s’utilitzen símbols i instruccions que més tard podran ser traduïdes a un llenguatge de programació concret.
Hi ha exemples de pseudocodi a l’apartat d’estructures bàsiques dels algorismes, però cal destacar la diferència entre assignació = i comparació ==. Assignació. L’expressió a = 3 significa que la variable anomenada “a” emmagatzema el valor 3.
Comparació. L’expressió a == 3 avaluarà si la variable a és igual al valor 3 i retornarà el valor vertader en cas afirmatiu, i fals en cas contrari.
Ordinogrames
Un ordinograme sempre té un únic punt d’inici i un únic punt de finalització. A més, tot camí d’execució ha de permetre arribar des de l’inici fins al final.
Les següents són accions prèvies a la realització del diagrama de flux:
- Identificar les idees principals a ser incloses en el diagrama de flux. Han d’estar presents el propietari o responsable del procés, els propietaris o responsables del procés anterior i posterior i d’altres processos interrelacionats, així com les terceres parts interessades.
- Definir què s’espera obtenir del diagrama de flux.
- Identificar qui ho farà servir i com.
- Establir el nivell de detall requerit.
- Determinar els límits del procés a descriure.
Els passos a seguir per construir el diagrama de flux són:
- Establir l’abast del procés a descriure. D’aquesta manera quedarà fixat el començament i el final del diagrama. Sovint el començament és la sortida del procés previ i el final l’entrada al procés següent.
- Identificar i llistar les principals activitats/subprocessos que estan inclosos en el procés a descriure i el seu ordre cronològic.
- Si el nivell de detall definit inclou activitats menors, llistar-les també.
- Identificar i llistar els punts de decisió.
Un ordinograma és un diagrama de flux que serveix per representar un algorisme. En ells es poden utilitzar els símbols de la taula següent.
| Símbol | Significat |
|---|---|
 |
Inici i fi de l’algorisme |
 |
Acció |
 |
Entrada o sortida |
 |
Decisió |
 |
Connector |
 |
Subrutina |
Estructures bàsiques dels algorismes
Els algorismes tenen tres tipus d’estructures:
- Estructures seqüencials: seguit de passos que es realitzen un rere l’altre.
- Estructures alternatives: En funció d’una determinada condició es realitzarà una o altra acció.
- Estructures repetitives: Una determinada acció o conjunt d’accions es repetiran fins que es complisca o es deixe de complir una determinada condició.
Estructures seqüencials
La seqüència d’ordres estarà expressada com a pseudocodi simplement col·locant les ordres una rere l’altra i en els ordinogrames encadenant-les amb fletxes:
acció1
acció2

Estructures alternatives
Alternativa simple (SI)
Un cert bloc de codi serà executat unicament si una determinada condició resulta ser vertadera:
si condició llavors
acció
fsi

Alternativa doble (SI-SINO)
També hi haurà una condició que pot ser vertadera o falsa, i dues accions: si la condició resulta vertadera es realitzarà una de les accions, i si es falsa es realitzarà l’altra:
si condició llavors
acció1
sino
acció2
fsi

Estructures repetitives
Iteració (MENTRE)
L’acció es realitzarà si una determinada condició es vertadera, i es continuarà repetint fins que aquesta condició siga falsa:
mentre condició fer
acció
fmentre

Iteració alternativa (PER-FINS)
L’acció es realitzarà fins que es complisca (o es deixe de complir) una determinada condició. En l’exemple següent, la variable index pren un valor inicial que va incrementant a cada repetició. L’acció es repetirà fins que index arribe a un cert valor final:
per índex = valor inicial fins valor final fer
acció
índex = índex + increment
fper

Eficència i complexitat algoritmica.
La tasca de la programació té com objectiu oferir algoritmes de resolució de problemes amb la major eficència possible.
Amb aquest objectiu bàsic sorgeixen diferents maneres de resoldre un mateix problema, oferint solucions alternatives.
Pot ser que no hi hagi una solució perfecte que sigui la més eficient per a totes les possibles problemàtiques. La complexitat de resolució es mida amb el paràmetre O(n) on s’avalua sempre pel pitjor cas d’execució de l’algoritme. podeu veure a l’enllaç diferents càlculs per esbrinar la complexitat de un algoritme.

Exemples d’algoritmes d’ordenació d’elements.
El problema sorgeix per la necessitat d’ordenar elements d’una llista.
El problema.
- Una llista com 8,4,2,3,4,5 volem que ens torni com 2,3,4,4,5,8.
- L’estructura bàsica que emprarem és un array de nombres (podria ser un array definit d’altres tipus de variables). Un array permet emmagatzemar dins una posició concreta (de 0 a N) una variables.
- Un array es sol representar com a A=[8,4,2,3,4,5] on A és el nom de la variable, cada un dels elements ocupa una posició. Començant de la posició 0 fins a la N.
- Un array té N+1 elements.
Una solució, L’algoritme d’inserció.
[one_half]
Algoritme d’ordenament mitjançant inserció.
i ← 1
while i < length(A)
j ← i
while j > 0 and A[j-1] > A[j]
swap A[j] and A[j-1]
j ← j - 1
end while
i ← i + 1
end while
La complexitat d’aquest algoritme és O(ne2).
on n és el nombre d’elements, si n=5 farà 25 voltes.
[/one_half]
[one_half_last]
Anàlisi, A=[8,4,2,3,4,5]
| i | j | A[j] | A[j-1] | Array |
|---|---|---|---|---|
| 1 | 1 | 4 | 8 | [4,8,2,3,4,5] |
| 2 | 2 | 2 | 8 | [4,2,8,3,4,5] |
| 1 | 2 | 4 | [2,4,8,3,4,5] | |
| 3 | 3 | 3 | 8 | [2,4,3,8,4,5] |
| 2 | 3 | 4 | [2,3,4,8,4,5] | |
| 1 | 4 | 3 | ||
| 4 | 4 | 4 | 8 | [2,4,3,4,8,5] |
| 3 | 4 | 3 | ||
| 2 | 3 | 4 | [2,3,4,4,8,5] | |
| 1 | 3 | 2 | ||
| 5 | 5 | 5 | 8 | [2,3,4,4,5,8] |
| 4 | 5 | 4 | ||
| 3 | 4 | 4 | ||
| 2 | 4 | 3 | ||
| 1 | 3 | 2 |
[/one_half_last]
[one_half]
Algoritme Merge Sort.
El algoritmo de ordenamiento por mezcla (merge sort en inglés) es un algoritmo de ordenamiento externo estable basado en la técnica divide y vencerás. Es de complejidad O(n log n).
function mergesort(m)
var list left, right, result
if length(m) ≤ 1
return m
else
var middle = length(m) / 2
for each x in m up to middle - 1
add x to left
for each x in m at and after middle
add x to right
left = mergesort(left)
right = mergesort(right)
if last(left) ≤ first(right)
append right to left
return left
result = merge(left, right)
return result
function merge(left, right)
var list result
while length(left) > 0 and length(right) > 0
if first(left) ≤ first(right)
append first(left) to result
left = rest(left)
else
append first(right) to result
right = rest(right)
if length(left) > 0
append rest(left) to result
if length(right) > 0
append rest(right) to result
return result
[/one_half]
[one_half_last]
Anàlisi del comportament de l’algoritme mergeSort sobre una llista de nombres A=[38,27,43,3,9,82,10]
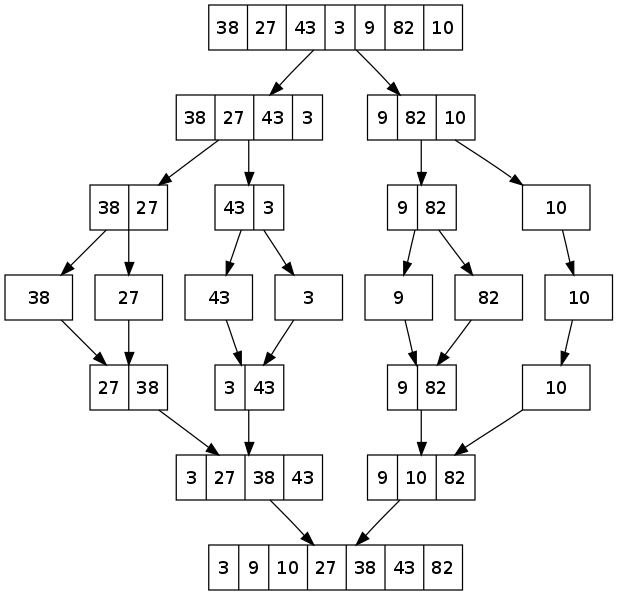
[/one_half_last]
Referències:
https://scorazon.perexat.net/~perexat/apuntsTIC/index.html
https://www.toptal.com/developers/sorting-algorithms/
http://solisgomez03.blogspot.com.es/2014/10/diagrama-de-flujo-en-programacion.html
https://en.wikipedia.org/wiki/Insertion_sort
http://aula.gimnesia.net/2017/12/05/u8-algoritmes/2on batxilleratLlenguatges de programació Un programa és un algorisme expressat de tal manera que un computador el pot entendre i executar. Hem insistit molt en el fet de que els computadors operen en llenguatge binari, i per a ells solament existeixen seqüències de 0 i 1. Per exemple, una operació bàsica...admin pereantonibennassar@gmail.comAdministratorAula de Informàtica
Ley de formación de números triangulares.
https://www.youtube.com/watch?v=hMFLIvvlpiY
http://visual6502.org/JSSim/index.html